Ejercicio 11 (Pt. 1): Análisis de la forma.

Análisis de la forma (Parte 1)

Martes, 27 de noviembre de 2018.

- En la clase de hoy hemos visto el último bloque de la asignatura, la forma. La forma es todo aquello que delimita un objeto y le distingue de su entorno, pudiendo ser natural o artificial.  Para entender mejor el concepto de forma la profesora ha puesto un documental bastante interesante sobre los tipos de forma que encontramos en la naturaleza.

- La naturaleza está regida por la matemática y la geometría, y es fascinante el darse cuenta de que absolutamente cada aspecto de la vida que nos rodea es cómo es por la matemática. Encontramos formas geométricas puras en la naturaleza pues es la manera más eficiente y cómoda de "existir". Vemos numerosos ejemplos increíbles como:

• Los panales de las abejas, los cuales son una sucesión de hexágonos perfectos. Científicos han investigado porqué las abejas saben que deben formar hexágonos para sus casas, del tamaño justo para ellas. ¿Por qué un hexágono y no triángulos o cuadrados? La respuesta está en que los hexágonos no dejan hueco entre sí, optimizando el espacio, y se necesita poca cantidad de cera para hacerlos. Es decir, eficiencia y optimización.

• Las burbujas, pompas. Muchas formas son esferas pues son muy eficientes, son infinitamente simétricas. Al igual que la forma esférica de la Tierra, las gotas de agua o incluso formas de vida como el plancton. La esfera es una forma muy estable. En el documental se mostraba de manera increíble cómo al juntar dos pompas se forma una más grande, buscando la forma más eficiente. Pero a medida que se iban juntando pompas, en el centro se crean formas como cuadrados y hexágonos, pues la estructura molecular de las pompas busca la manera más eficiente de permanecer más estable.

• Hexágonos en formaciones rocosas.

• Cristales de sal cuya estructura molecular hace que adopten una forma de ángulo recto, formando cubos perfectos.

• Las proteínas también tienen una estructura geométrica, pues forman cilindros, hexágonos, pentágonos y cilindros. Estas moléculas han buscado la manera más eficiente de organizarse y de mantener intacta su estructura.

- Como vemos, las formas de la naturaleza tienden a adoptar formas geométricas pues es lo más eficaz para su optimización. Destaca el ejemplo del arquitecto Frei Otto, el cual supuso una revolución para la arquitectura al inspirarse en estas formas de la naturaleza, perfectas y eficientes.

- Desde la Antigüedad Clásica el hombre ha buscado crear cosas que resulten totalmente armónicas y perfectas al ojo humano, y esto es debido a que a nuestro cerebro le causa satisfacción ver cosas absolutamente simétricas, genera armonía visual. Por el contrario, el cerbero interpreta como erróneo aquello que no es simétrico, generando en nosotros una sensación de rechazo. Siguiendo esta idea, los griegos idearon la geometría, para así buscar el código por el cual se rigen las formas de la naturaleza. 

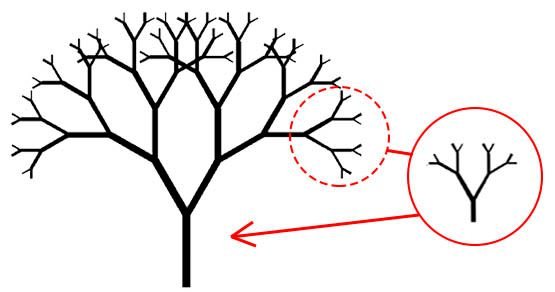
- Sin embargo, la búsqueda de este código no es tan sencilla pues no todo es perfecto y simétrico en la naturaleza. De hecho, encontramos formas imperfectas como los copos de nieve o las ramas de los árboles. No obstante, en este caos imperfecto también se han encontrado patrones simétricos y armónicos. Es lo que se conoce como las matemáticas fractales. Esta teoría nos habla de un patrón que se repite a distintas escalas. Este rasgo puede verse en elementos de la naturaleza que a primera vista pueden parecer asimétricos e irregulares como son los árboles, los copos de nieve, las neuronas...

- Es muy curioso como es nombrado el nombre del rompedor artista tachista Jackson Pollock. Un artista matemático ha estudiado las obras de Pollock, obras aparentemente irregulares y sin sentido alguno. Sin embargo, se ha descubierto que los cuadros de Pollock siguen unos patrones fractales que de alguna manera crean obras simétricas a su manera. No imagino cómo pudo surgir tal cosa ya que el artista se limitaba a salpicar sus lienzos de manera aleatoria, pero al parecer no es así.

- También vemos el ejemplo del co-fundador de Pixar, quién supuso una revolución para el mundo de las animaciones al crear un paisaje montañoso mediante el uso de triangulos fractales.

- Para acabar de consolidar lo visto, la profesora nos hizo un breve test para comprobar si habíamos comprendido el documental. El test se componía únicamente de tres preguntas.

- Concluyendo, un documental cuanto menos interesante y fascinante. Uno se queda totalmente boquiabierto al descubrir como la matemática rige nuestra existencia, y en cómo la más absoluta imperfección sigue unos patrones perfectos.